False Position Method using C programming
Suppose we are given the continuous function f(x) in the interval [p, q] and we want to find root of the equation f(x)=0 by false position method. The process is described as follows:-
1) Find two points a and b such that f(a) * f(b) < 0.
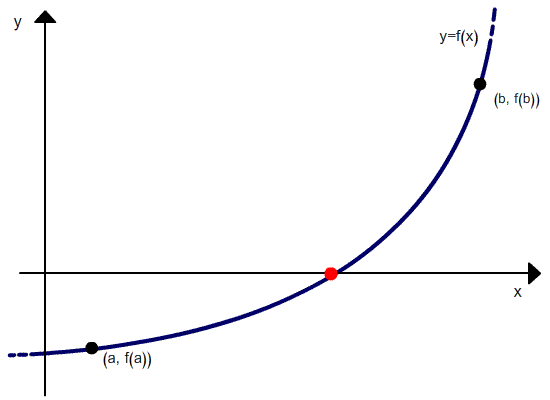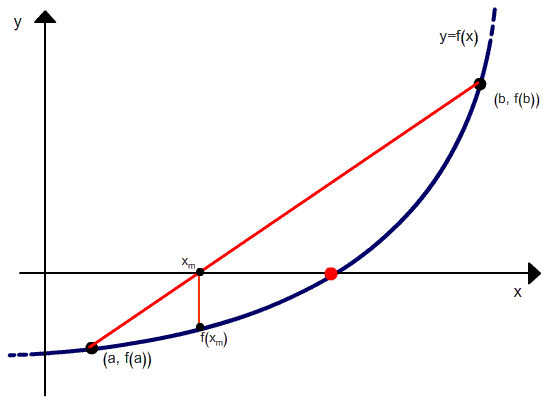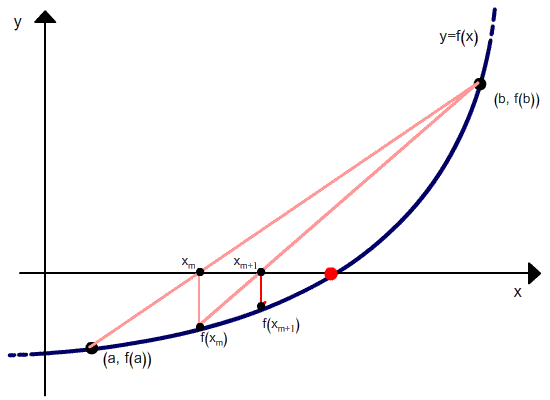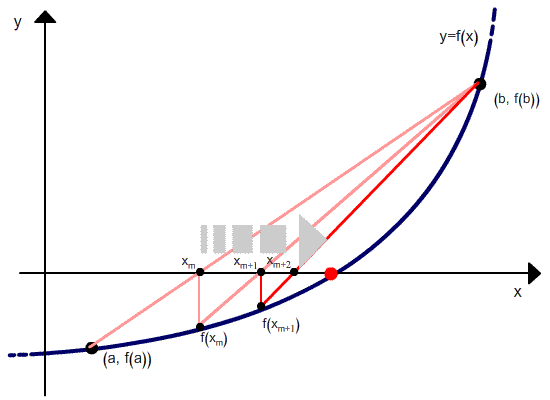
2) Compute c= (af(b)-bf(a))/(f(b)-f(a)).
3) If f(c) = 0 then ‘c’ is the required root & stop the process if f (c) 0 then go to next step.
4) If f(a) * f (c) <0 then root lies between a & c otherwise the root lies between c & b.
5) Repeat step (2), (3) and (4) until the root is found to be desired of accuracy.
#include<stdio.h>
#include<conio.h>
#include<math.h>
float f(float x){
return (x*log10(x)-1.2);
}
void main(){
int i,n;
float a,b,c;
clrscr();
printf(“Enter the no of iteration:”);
scanf(“%d”,&n);
printf(“enter two values where the root lies:”);
scanf(“%f %f”,&a,&b);
if(f(a)*f(b)>0)
{
printf(“the initial values are out of range”);
getch();
exit(0);
}
else{
for(i=1;i<=n;i++){
c=(a*f(b)-b*f(a))/(f(b)-f(a));
if(f(c)==0)
break;
if(f(a)*f(c)<0)
b=c;
else
a=c;
}
printf(“the reqd. root is:%f”,c);
getch();
}
}